tools »

10 - Numpy应用案例[3]

#tools   #programming   #Numpy  

---

Table of Content

“去极值是量化分析预处理中不可或缺的一步。在各种方法中，中位数拉回法因其鲁棒性和适应性广泛应用。通过 Numpy 的向量化实现，我们可以轻松完成多资产的去极值操作，显著提升计算效率。”

---

向量化又一例: 多资产中位数去极值

去极值是量化分析预处理中的常见步骤，在机器学习中也很常见。在各种去极值方法中，中位数拉回是对数据分布特性适应性最广、最鲁棒的一种。

我们先介绍绝对中位差（median absolute deviation）的概念：

\[MAD = median(|X_i - median(X)|)\]

为了能将 MAD 当成与标准差\(\sigma\)相一致的估计量，即 \(\(\hat{\sigma} = k. MAD\)\)

这里 k 为比例因子常量，如果分布是正态分布，可以计算出： $$ k = \frac{1}{(\Phi^{-1}(\frac{3}{4}))} \approx 1.4826 $$

基于这个 k 值，取 3 倍则近似于 5。

代码实现如下：

from numpy.typing import ArrayLike

def mad_clip(arr: ArrayLike, k: int = 3):
    med = np.median(arr)
    mad = np.median(np.abs(arr - med))

    return np.clip(arr, med - k * mad, med + k * mad)

---

np.random.seed(78)
arr = np.append(np.random.randint(1, 4, 20), [15, -10])
mad_clip(arr, 3)

这段代码只能对单一资产进行mad_clip。如果要同时对A股所有资产的某种指标去极值，上述方法需要循环5000多次，显然速度较慢。此时，我们可以使用下面的方法：

def mad_clip(df: Union[NDArray, pd.DataFrame], k: int = 3, axis=1):
    """使用 MAD 3 倍截断法去极值"""

    med = np.median(df, axis=axis).reshape(df.shape[0], -1)
    mad = np.median(np.abs(df - med), axis=axis)

    magic = 1.4826
    offset = k * magic * mad
    med = med.flatten()
    return np.clip(df.T, med - offset, med + offset).T

这一版的 mad_clip 可以接受 numpy ndarray 和 pandas dataframe 作为参数。输入的数据格式是什么，它返回的数据格式就是什么。

我们在np.median调用中，传入了 axis参数。如果axis=0, 表明按列的方向遍历，因此是按行取中位数；axis=1,表明按行的方向遍历，因此是按列取中位数。

我们使用真实数据测试一下：

---

# 加载测试数据
start = datetime.date(2023, 1, 1)
end = datetime.date(2023, 12, 29)
barss = load_bars(start, end, 7)

closes = barss["close"].unstack("asset").iloc[-5:]
closes

输出数据为：

asset/date	002095.XSHE	003042.XSHE	300099.XSHE	301060.XSHE	601689.XSHG	603255.XSHG	688669.XSHG
2023-12-25	23.400000	18.090000	6.10	13.00	73.910004	36.799999	18.080000
2023-12-26	21.059999	17.520000	5.94	12.83	72.879997	37.000000	18.080000
2023-12-27	20.070000	17.590000	6.04	12.84	72.000000	36.840000	18.049999
2023-12-28	20.010000	18.139999	6.11	13.14	72.199997	38.150002	18.440001
2023-12-29	20.270000	18.580000	6.19	13.29	73.500000	37.299999	18.740000

为了测试效果，我们将k设置为较小的值，以观察其效果：

mad_clip(closes,k=1)

asset/date	002095.XSHE	003042.XSHE	300099.XSHE	301060.XSHE	601689.XSHG	603255.XSHG	688669.XSHG
2023-12-25	23.400000	18.090000	10.217396	13.00	25.962605	25.962605	18.080000
2023-12-26	21.059999	17.520000	10.296350	12.83	25.863649	25.863649	18.080000
2023-12-27	20.070000	17.590000	10.325655	12.84	25.774343	25.774343	18.049999
2023-12-28	20.010000	18.139999	10.582220	13.14	26.297781	26.297781	18.440001
2023-12-29	20.270000	18.580000	10.659830	13.29	26.820169	26.820169	18.740000

我们看到，原始数据中的73.9被拉回到25.9，6.1被拉回到10.2(以第一行为例)，并且都是以行为单位计算的。

---

min_range: 多少周期以来的最小值？

这是一个很常见的需求，比如，有股谚语云，天量见天价，地量见地价。当行情处在高位，成交量创出一段时间以来的天量之后，后续成交量将难以为继，容易引起下跌；当行情处在低位，成交量创出一段时间以来的地量之后，表明市场人气极度低迷，此时价格容易被操纵，从而引来投机盘。

在通达信公式中有此函数，在麦语言中，对应的方法可能是LOWRANGE。以下是myTT中LowRange函数的实现：

def LOWRANGE(S):                       
    # LOWRANGE(LOW)表示当前最低价是近多少周期内最低价的最小值 by jqz1226
    rt = np.zeros(len(S))
    for i in range(1,len(S)):  rt[i] = np.argmin(np.flipud(S[:i]>S[i]))
    return rt.astype('int')

这是一个看似简单，但实际上比较难实现的功能。如果我们对上述函数进行测试，会发现它不一定实现了需求（也可能是本文作者对此函数理解有误）。

s = [ 1, 2, 2, 1, 3, 0]

LOWRANGE(np.array(s))

在上述测试中，我们希望得到的输出是[1, 1, 1, 3, 1, 6]，但LOWRANG将给出以下输出：

---

array([0, 0, 0, 2, 0, 0])

下面，我们给出该函数的向量化实现。

Warning

该函数在开头的几个输出中，存在出错可能。不影响因子分析，暂未修复。

def min_range(s):
    """计算序列s中，元素i是此前多少个周期以来的最小值

    此方法在个别数字上有bug

    Example:
        >>> s = np.array([5, 7, 7, 6, 5, 8, 2])
        >>> min_range(s)
        array([1, 2, 1, 2, 3, 1, 6])
    """
    n = len(s)

    # handle nan
    filled = np.where(np.isnan(s), -np.inf, s)
    diff = filled[:,None] - filled
    mask = np.triu(np.ones((n, n), dtype=bool), k=1)
    masked = np.ma.array(diff, mask=mask)

    rng = np.arange(n)
    ret = rng - np.argmax(np.ma.where(masked > 0, rng, -1), axis=1)
    ret[0] = 1
    if filled[1] <= filled[0]:
        ret[1] = 2
    return ret

---

s = np.array([5, 7, 7, 6, 5, 8, 2])
min_range(s)

最终输出的结果是：

array([1, 1, 2, 3, 4, 1, 6])

在第2个7的位置，输出与期望不一致，但此后计算都正确。这个实现非常有技巧，运用了三角矩阵做mask array，从而消解了循环。

均线计算：SMA和分时均线

使用numpy计算移动均线非常简单，使用np.convolve()即可。

def moving_average(ts: ArrayLike, win: int, padding=True)->np.ndarray:
    kernel = np.ones(win) / win

    arr = np.convolve(ts, kernel, 'valid')
    if padding:
        return np.insert(arr, 0, [np.nan] * (win - 1))
    else:
        return arr

moving_average(np.arange(5), 3)

输出结果为array([nan, nan, 1., 2., 3.])

---

移动均线是只考虑价格信息的一种均线。分时均价线则则同时纳入成交量和成交价信息的均线，在日内交易中有特别重要的含义。比如，在市场不好的情况下，如果个股价格位于分时均线下方，此前两次上冲均线失败，那么，一旦冲第三次失败，一般认为要尽快卖出。反之亦然。

均价线的计算如下：

如果当前时刻为t，则用开盘以来，直到时刻t为止的成交金额除以成交量，即得到该时刻的累积成交均价。将所有时刻的成交均价连接起来，即构成了分时均价线。

这个功能看似复杂，但由于numpy提供了cumsum函数，因此实际上计算非常简单：

def intraday_moving_average(bars: DataFrame)->np.ndarray:
    acc_vol = bars["volume"].cumsum()
    acc_money = barss["amount"].cumsum()

    return acc_money / acc_vol

在本环境中，只提供了日线数据，我们以日线代替分钟线进行测试：

start = datetime.date(2023, 1, 1)
end = datetime.date(2023, 12, 29)
barss = load_bars(start, end, 1)

intraday_moving_average(barss)

---

计算最大回撤

最大回撤（MDD）是指投资组合从最高点到最低点的最大观察损失，直到达到新的最高点。最大回撤是一定时间周期内的下行风险指标。

\[ MDD = \frac{Trough Value - Peak Value}{Peak Value} \]

max drawdown是衡量投资策略风险的重要指标，因此，在empyrical库中有实现。不过，作为策略风险评估指标，empyrical没必要返回duration等信息，也没有实现滑动窗口下的mdd。现在，我们就来实现滑动版本。

# https://stackoverflow.com/a/21059308
from numpy.lib.stride_tricks import as_strided
import matplotlib.pyplot as plt

def windowed_view(x, window_size):
    """Creat a 2d windowed view of a 1d array.

    `x` must be a 1d numpy array.

    `numpy.lib.stride_tricks.as_strided` is used to create the view.
    The data is not copied.
    Example:

    >>> x = np.array([1, 2, 3, 4, 5, 6])
    >>> windowed_view(x, 3)
    """

---

    """
    array([[1, 2, 3],
           [2, 3, 4],
           [3, 4, 5],
           [4, 5, 6]])
    """
    y = as_strided(x, shape=(x.size - window_size + 1, window_size),
                   strides=(x.strides[0], x.strides[0]))
    return y

def rolling_max_dd(x, window_size, min_periods=1):
    """Compute the rolling maximum drawdown of `x`.

    `x` must be a 1d numpy array.
    `min_periods` should satisfy `1 <= min_periods <= window_size`.

    Returns an 1d array with length `len(x) - min_periods + 1`.
    """
    if min_periods < window_size:
        pad = np.empty(window_size - min_periods)
        pad.fill(x[0])
        x = np.concatenate((pad, x))
    y = windowed_view(x, window_size)
    running_max_y = np.maximum.accumulate(y, axis=1)
    dd = y - running_max_y
    return dd.min(axis=1)

np.random.seed(0)
n = 100
s = np.random.randn(n).cumsum()
win = 20
mdd = rolling_max_dd(s, win, min_periods=1)

plt.plot(s, 'b')
plt.plot(mdd, 'g.')
plt.show()

测试表明，当时序s长度为1000时，rolling_max_dd的计算耗时为100𝜇S。

滑动窗口下，生成的mdd与原序列对照图如下：

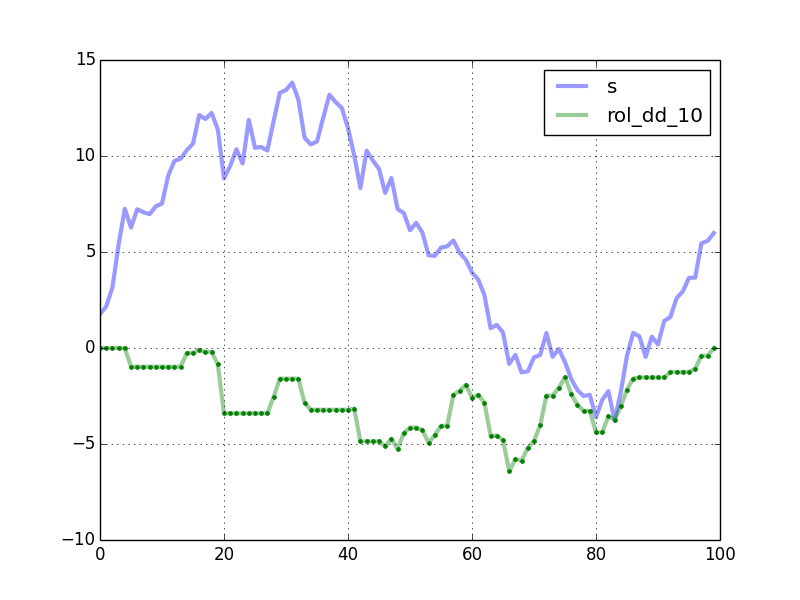
该方法中，还简单地封装了一个将一维数组转换为滑动窗口视图的函数，可以在其它地方使用。

---

寻找自适应参数

很多基于技术指标的交易策略往往指定了固定的阈值。比如，一些人会在RSI 80以上做空，在RSI 20以下做多。即使是用在指数和行业板块上，这样的指标仍然不够精确，因为在上行通道中，RSI的顶点会高于下行通道中的RSI顶点；在下行通道中，RSI的底部则会比上行通道中的RSI底部低很多。

此外，不同的标的，RSI取值范围也不一样。不仅仅是RSI，许多技术指标都存在需要根据当前的市场环境和标的，采用自适应参数的情况。

其中一个方案是使用类似于布林带的方案，使用指标均值的标准差上下界。但这个方案隐含了技术指标均值的数据分布服从正态分布的条件。

我们可以放宽这个条件，改用分位数，即numpy的percentile来确定参数阈值。

%precision 2

from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"

np.random.seed(78)
s = np.random.randn(100)

hbound = np.percentile(s, 95)
lbound = np.percentile(s, 5)

---

s[s> hbound]
s[s< lbound]

通过percentile找出来超过上下界的数据，输出如下：

array([2.09, 2.27, 2.21, 2.12, 2.19])
array([-1.68, -2.4 , -1.97, -1.7 , -1.46])

一旦指标超过95%的分位数（hbound），我们就做空；一旦指标低于5%的分位数（lbound），我们就做多。

这里我们也可以使用中位数极值法。一旦指标超过中位数MAD值的3倍，就发出交易信号 。